Giocare e pensare 2003
GARA DI MATEMATICA
| Home |
![]()
| Rispondere al maggior numero possibile delle domande proposte, a scelta del concorrente. Viene indicato per ogni domanda il punteggio massimo ottenibile rispondendo in modo ottimale alla domanda stessa. E' essenziale spiegare bene il perchè di ogni affermazione, dal momento che nell' assegnazione del punteggio verrà tenuto conto oltre che dalla correttezza del risultato anche della pulizia e del rigore delle spiegazioni. Buon lavoro! | |
| 1. Una popolazione di un numero ignoto di individui e' divisa in un numero parimenti ignoto di partiti. Ogni individuo e iscritto a uno e un solo partito, di cui conosce I' esatto numero di iscritti. Per valutare quale e' il numero medio di membri dei partiti si chiede ad ogni individuo il numero di iscritti al suo partito e poi si fa la media aritmetica. Discutere la validità di questo modo di procedere supponendo che tutti rispondano in modo veritiero. (punti 5) | |
| 2. Quale è il numero minimo di sorgenti puntiformi necessarie per illuminare completamente dall' esterno una palla sferica se non ci sono vincoli sulla loro posizione e distanza dalla palla? (punti 5) | |
| 3. La somma di un euro e' stata investita all' inizio dell' anno 1 all' interesse composto annuo del 5% e viene ritirata, con tutti gli interessi maturati all' inizio dell' anno 2003. Stimare, anche grossolanamente, quanti euro sono ritirati. (punti7) | |
| 4.
Dire quante soluzioni ha il seguente problema: PROBLEMA: Un pastore ha 10 pecore e 10 capre. Quanti anni ha il pastore? (punti 3) |
| 5.
Pierino trova un testo di cui sono leggibili solo le prime righe.
Esse sono: "Quante soluzioni ha il seguente problema: "PROBLEMA: Quante soluzioni ha il seguente problema''1 PROBLEMA: Una nave si trova....." " Pierino dice di saper rispondere nonostante il testo sia gravemente incompleto. E' possibile? (punti 2). |
|
| 6. Un personaggio vi propone la seguente scommessa. Estrarra' a sorte lanciando una moneta non truccata uno tra due bastoncini di lunghezza a voi ignota e poi lo spezzerà in due scegliendo a caso i! punto di rottura in modo che ogni punto del bastoncino abbia le stesse probabilità degli altri di essere scelto. Se sarà possibile costruire un triangolo che abbia per i lati i due pezzi ottenuti e il terzo bastoncino vincerete un euro, se no perderete un euro a. Vi conviene accettare la scommessa? (punti 3) b. Quale rapporto tra le lunghezze dei due bastoncini ritenete sia il più vantaggioso per voi? (punti 4) c. Quale rapporto tra le lunghezze dei due bastoncini ritenete sia il piu' vantaggioso che vi propone la scommessa? (punti 3) | |
| 7. Un cacciatore inseguendo un orso percorre 1 chilometro a sud, uno a est ed uno a nord. A questo punto uccide l' orso e si rende conto di essere tornato al punto di partenza. Di che colore e- 1' orso? (punti 8) | |
|
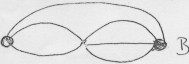
8. Un viaggiatore vuole andare dalla città ' A alla citta' B, collegate da strade secondo lo schema
Ogni tratta è bloccata dalla neve con probabilità 1/3, indipendentemente dalle altre. Qual è la probabilità che riesca ad effettuare il viaggio? (punti 4) |