Appendice schematica sul metodo numerico

Esistono vari algoritmi che approssimano diversamente il valore dell’accelerazione e della velocità. Molti di questi sono più accurati dell'algoritmo di Eulero che abbiamo appena descritto. La formula utilizzata dal metodo di Eulero può essere derivata dallo sviluppo di Taylor, che consente di calcolare il valore della funzione f(t+D t), con un grado di approssimazione qualsiasi, a partire dalla conoscenza del valore della funzione nel punto t, fx(t) e del valore delle derivate della funzione nello stesso punto:

f(t+D t) =

con t<x <t+D t. Per n=1 si ha:

f(t+D t) = f(t)+ D t

e questo valore approssimato è affetto da un errore di troncamento che dipende dal quadrato dell’intervallo di integrazione:

Per il generico intervallo ti« ti+1=(ti +D t) avremo: f(ti+1)=f(ti)+v(ti) D t e per n=2 si ha:

f(t+D t) = f(t)+ D t +

e che è approssimata con un errore di troncamento che dipende dal cubo dell’intervallo di integrazione:

.

Per risolvere le equazioni differenziali del primo ordine si usa lo sviluppo in serie di Taylor, poiche’, in base alla conoscenza analitica della derivata prima della funzione (data dall'equazione da risolvere), si possono calcolare le sue derivate di ordine superiore (ottenute mediante derivazioni successive dell'equazione da risolvere) e quindi, se questo calcolo non diventa troppo complicato, si puo’ calcolare il valore della funzione approssimato a qualsiasi ordine. Si noti che se la prima volta che si applica il metodo, per determinare f(t0+Dt), il valore di f(to) e' conosciuto esattamente, gia' la seconda volta, per calcolare per esempio f(to+2 Dt), il valore del primo termine della serie e' approssimato.
L’altro uso che si fa delle serie di Taylor , che coincide con quello esposto nella parte iniziale di questa scheda, e’ di riscrivere la derivata che compare nelle equazioni come rapporto incrementale (con possibili correzioni successive. Infatti per risolvere mediante integrazione numerica una equazione differenziale del secondo ordine, si sosituisce l'equazione del II ordine con un sistema di equazioni differenziali del primo ordine (la stessa tecnica e' usata, anche, in qualche caso per trovare la soluzione analitica). Ovvero data l'equazione

si introduce la funzione v(t) =ds/dt ( che e’ anch’essa da determinare) e si considera il sistema:

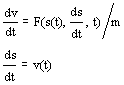
con condizioni iniziali s(to)=so, v(to)=vo= (ds/dt )t=to.

In entrambe le equazioni le derivate possono essere approssimate da uno sviluppo di Taylor arrestato al primo ordine

f(t+D t) = f(t)+ D t

e si considera ogni derivata espressa dalla funzione

=( f(t+D t) - f(t))/ D t,

che implica approsiinmare la derivata al primo ordine in D t (metodo di Eulero semplice). Si può verificare per sostituzione in questo caso si ottengono le espressioni (8) e (9). Le espressioni (4) e (5) invece corrispondono a una approssimazione piu’ complessa, in cui l’equazione per la velocita’ viene approssimata come detto sopra, mentre per la seconda equazione, si considera che la derivata nel punto di mezzo dell’intervallo di tempo D t, e’ data


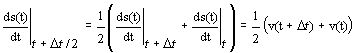
e

e si tiene conto del fatto che che implica approssimare la derivata al II ordine in t, come si puo’ facilmente trovare considerando la somma de gli lo somma degli sviluppi di Taylor per s(t+t) e per s(t-t).

Bibliografia in italiano Collana Schaum, Analisi numerica
Bevilacqua, Bini, Capovani,Menchi "Introduzione alla matematica computazionale"-Zanichelli.